Over the past few weeks I’ve been designing compute kernels for a Convolutional Neural Network (CNN). This will run on my chip, where I have access to an array of compact SIMD VLIW processors (the AMD AI Engine). The gist of it is that anything written for these processors will be parallelized nicely because they support instructions that do so.
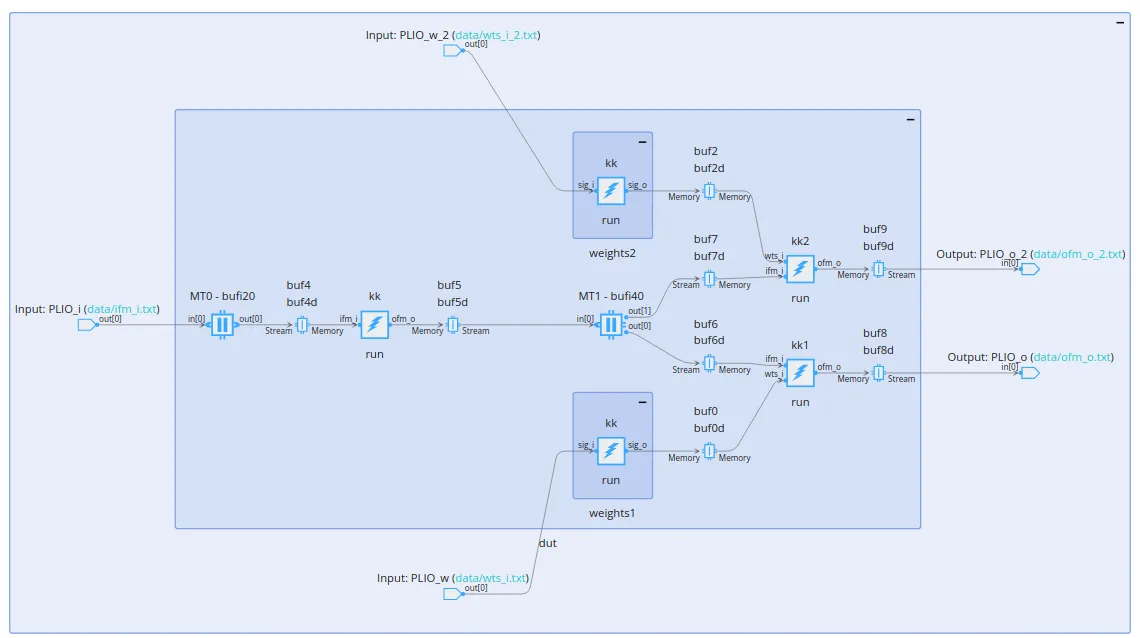
Now let’s say, for simplifcation, that each processor only does one thing (a kernel, if you will). We want to organize our kernels to run in parallel, this is abstracted as a graph; a Kahn process network, to be specific. A node connects to another node to indicate that it requires a resource, so nodes at the same level can run in parallel (more or less). Below is the computation graph (before some optimization) for the first two convolution layers of my CNN:

The little squares with the lightning bolts are the kernels, so what’s the rest? Well, this is a hardware model after all, so we need memory. The idea behind having an array of those little processors is to “compute-in-memory”, specifically, IBM has shown that this is particularly effective when running neural networks (something dubbed neuromorphic computing, mimicking the brain structure). The kernel program memory is actually not that big, only 16 kB, so we should have a bunch of memory around anyways. There are two types of memory here, buffers and memory tiles, storing up to 64 and 512 kB respectively.
The operation we’ll be performing on this input is convolution. As a quick reminder, the operation consists of sliding a rectangular filter over the input and adding the elementwise products in the patch like so:
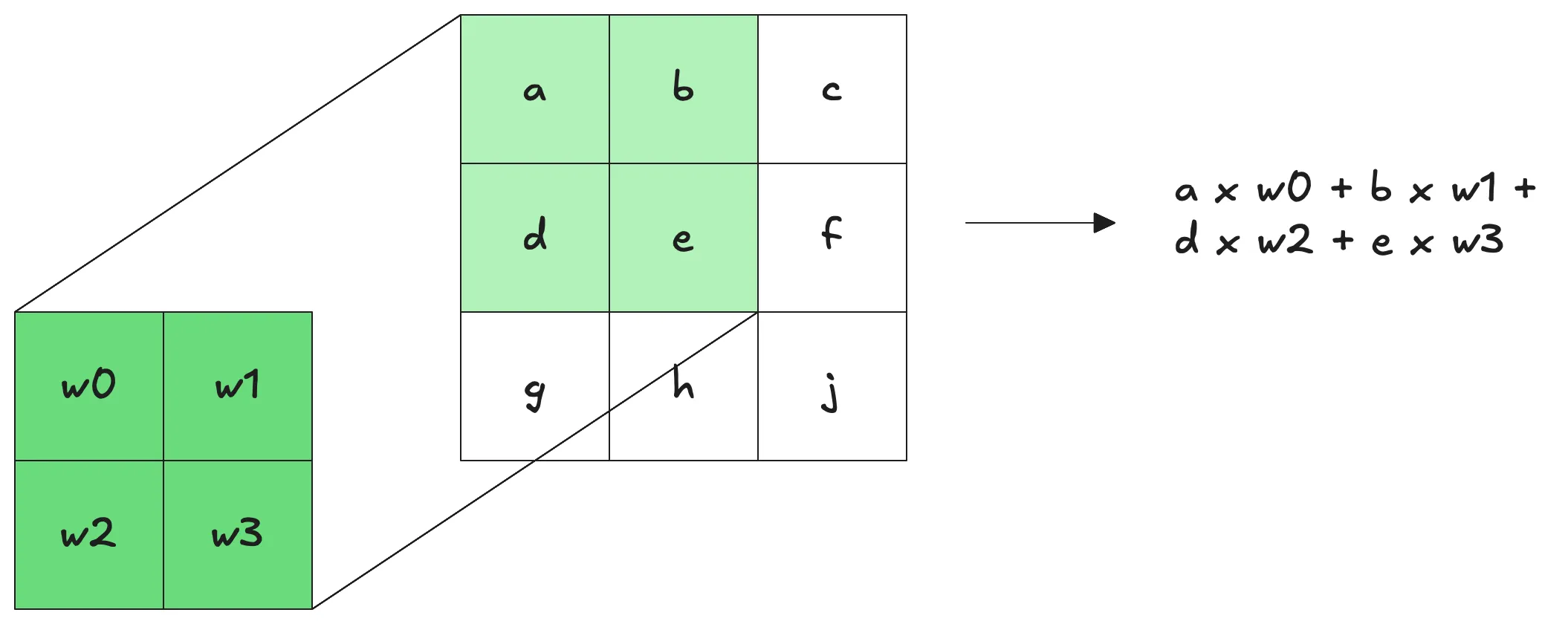
This generalizes over multiple channels as you’d expect. Sliding the filter over the input produces one layer for the output, and with multiple filters (different rectangular sets of weights) we can control that output dimension.
Now for my CNN, the first input is 580x196 UINT8s (about 100k bytes). That’s obviously too much for any kernel or buffer, so we need some memory tiles. One thing that’s pretty interesting about the memory tiles is that we can declare how the reading and writing operations are addressed (I’ve talked about addressing tensors before). You can imagine how the sliding operation in convolution can lead to some pretty annoying arithmetic. Thankfully, the API makes this trivial in the memory tile, we can just read as follows:
// the parameters here are (full size, num inputs, num outputs)mt_input_buf = shared_buffer<uint8>::create({580*196*1},1,1);read_access(mt_input_buf.out[0]) = tiling({ .buffer_dimension = {580,196}, .tiling_dimension = {6,6}, .offset = {0,0}, .tile_traversal = {{.dimension=0,.stride=2,.wrap=288}, {.dimension=1,.stride=2,.wrap=96}} });I want to highlight here one of the first important design choices we had to make. If you’re familiar with convolution, the filter size of 6x6 might seem a bit unusual. Initially we had this as 5x5 filter, but that led to odd numbered dimensions in the later layers, and this caused memory alignment issues. To avoid that, we worked backwards to find numbers that kept everything even and the CNN performant, this worked out ok, so crisis averted, right?
Well, unfortunately we run into another problem. We have 16 filters, so the output of this convolution layer is 288x96x16 (about 400k elements); we need another memory tile. Thinking ahead, this will feed into a MaxPool layer to reduce the dimensionality to 144x48x16, and this will need another memory tile too.
Besides resource allocation, there’s another, deeper issue lying underneath. For every memory tile,
the associated kernel takes a repetition_count, which is supposed to specify how many times that memory tile is used, or how many times the kernel runs. For this one, it should simply
be 288x196.
The MaxPool layer poses a problem now because it has to wait to gather four outputs of the first layer before it can spit out its own output. In reality, it has to wait even longer
because our layer is going row by row, so it actually has to wait for a full row and a little bit longer.
This, in and of itself, is actually fine, because we’re storing in a memory tile. The read access specification will make it so that it waits until its tiling_dimension is full, no problem.
The problem lies in the full picture of the graph; the second convolution layer, after MaxPool, does not need to wait. In other words, it will be
consuming from the MaxPool memory tile faster than the kernel is producing.
At the heart of this production-consumption rate mismatch is the fact we have to wait a full row of the first convolution layer, so I decided to tackle the problem on this front. Consider instead sliding an 8x8 patch over the input. Along this 8x8 patch, we can apply the original 6x6 filter to obtain 2 row outputs and 2 columns outputs, like this:
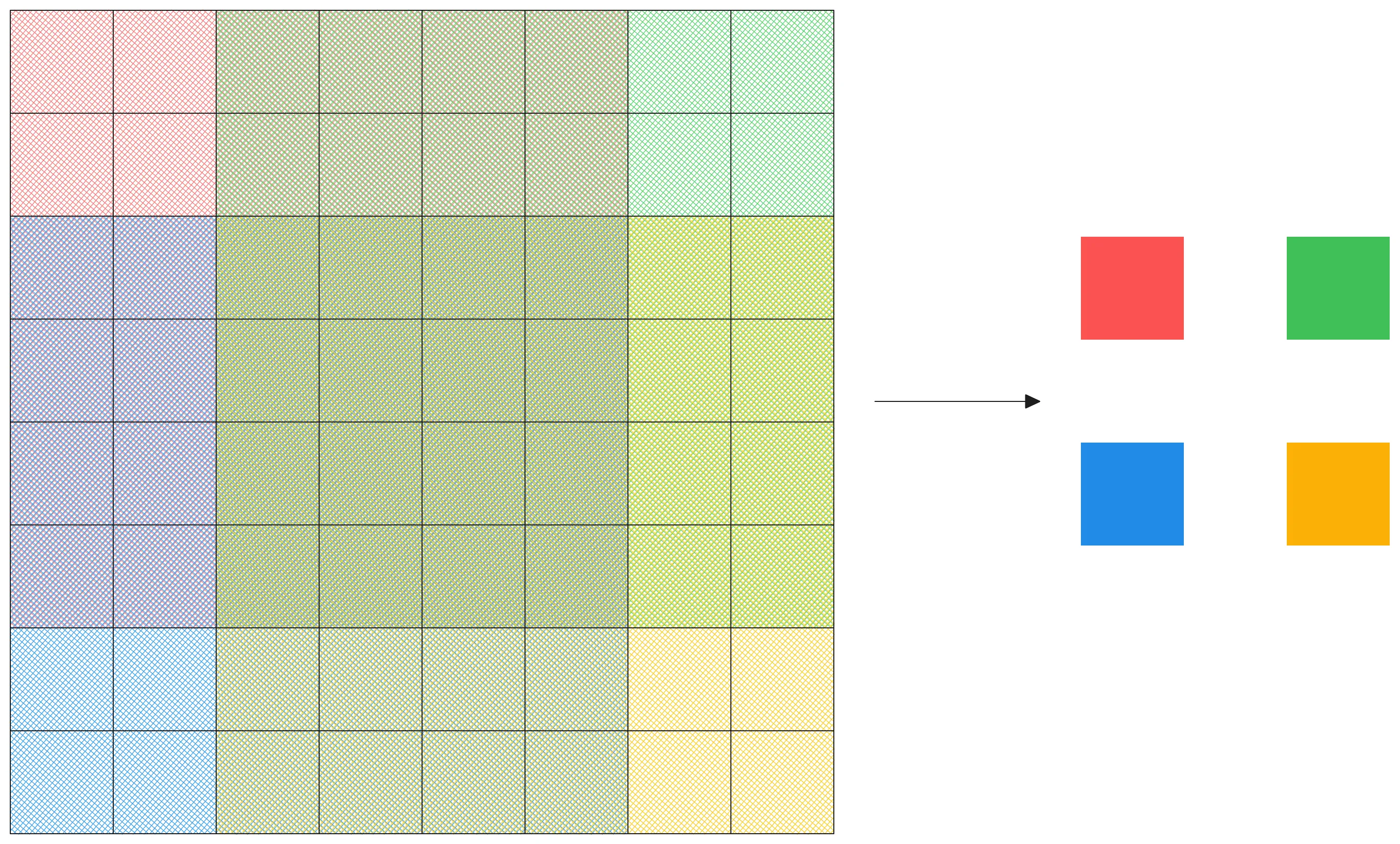
Now the outputs here correspond precisely to the 2x2 window we’ll be Max Pooling, so we can move all of this into the same kernel, and its production rate will match the second convolution layer output rate. Note that our stride now should be four, so the new params are:
// the parameters here are (full size, num inputs, num outputs)mt_input_buf = shared_buffer<uint8>::create({580*196*1},1,1);read_access(mt_input_buf.out[0]) = tiling({ .buffer_dimension = {580,196}, .tiling_dimension = {8,8}, .offset = {0,0}, .tile_traversal = {{.dimension=0,.stride=4,.wrap=144}, {.dimension=1,.stride=4,.wrap=48}} });With that in mind, we can start writing our first kernel.
One important consideration here is that a convolution naturally uses predefined weights. ThisThe first layer will have
sixteen 6x6 filters amounting to 576 total weights; 592 total elements with the biases. Thankfully, this is a small amount that we can completely store in program memory, with the usual care for alignment:
alignas(aie::vector_decl_align) bfloat16 weights[576] = {...};alignas(aie::vector_decl_align) bfloat16 biases[16] = {...};Now we should think about our loops. This kernel will have an 8x8 input patch, but we’ll actually process four 6x6 patches inside it, and repeat this for every filter. Naively, we might want the following loop structure:
for (int i=0; i < 16; i++){ for (int j=0; j < 4; j++) { for (int k=0; k < 36; k++){} }}Going back to our memory model, there are memory tiles and buffers. The graph compiler will arrange an 8x8 buffer as an input to the kernel, in row major order, which we have to access with pointers. You can imagine that the pointer arithmetic doesn’t behave nicely with those loops. So what can we do?
First let’s do something about iterating over all 16 output channels. We have a vector processor with accumulator registers after all. The result, for each filter, will be a sum over 36 products, 4 times over different windows. The stride is 2, so we can imagine something like this:
// vertical stridefor (int rr=0; rr < 4; rr += 2){ // horizontal stride for (int cc=0; cc < 4; cc += 2) { // initialize a 16 accumulator for all output channels at once aie::accum<accfloat,16> acc = aie::zeros<accfloat,16>(); for (int k=0; k < 36; k++) {} // ... }}It is now worth considering how exactly we intend to get the 36 elements from the 6x6 patch; zooming out, how we’re iterating
over the 8x8 patch as a whole. Fortunately for us, 8 is a power of 2, which means we can open a vector iterator over the input buffer.
If we have it = aie::begin_restrict_vector<8>(input_buf);, it++ goes down a full row which makes this aspect of the pointer arithmetic much easier. We can now add
it += 2 at the end of the rr loop comfortably.
Hopefully the pieces have fallen into place and you realize how we can do the innermost loop (hint: we will break the 36 into 6 rows using the vector iterator and 6 columns along the vector). All of this should net us a single element of the 8x8 patch. This should multiply with the weight of a single filter, and repeatedly add all the products together. But remember that 16-accumulator? Well we can compute all 16 filter outpus at once with it. The “multiply-and-accumulate” (MAC) operations are precisely what we want, and when passed an accumulator with multiply lanes, the sums are stored individually:
constexpr auto aie::mac(const Acc &acc, const Vec1 &v1, const Vec2 &v2)// more or less thisfor (unsigned i = 0; i < Elems; ++i) out[i] = acc[i] + v1[i] * v2[i];Because our processors support SIMD, this should compile into a single instruction that executes all the operations in parallel
(aie::mac is actually an API over the intrinsics, the right one would be something like mac_elem_16).
We still have a little bit left, but it’s easy. Our input is “flat” in the amount of channels, but we want to multiply with a 16-vector.
Another common vector operation is broadcast, which takes a scalar and spreads it across a vector, so we just do that.
After the 36 products we should also add the biases. Then all that’s left is saving
four results across rr and cc, and then at the end taking the maximum—remember, we want the MaxPool.
Putting it all together, the kernel function is:
void conv2d::filter_6x6( input_buffer<uint8> &input_buf, output_buffer<bfloat16> &output_buf){ auto it = aie::begin_restrict_vector<8>(input_buf); auto out = aie::begin_restrict_vector<16>(output_buf); // we'll store the 4 conv outputs here std::array<aie::vector<bfloat16,16>,4> convs; // and we'll keep track of the above with this int conv_num = 0;
for (int rr=0; rr < 4; rr += 2) { for (int cc=0; cc < 4; cc += 2) { aie::accum<accfloat,16> acc = aie::zeros<accfloat,16>(); // weights iterator auto itw = aie::begin_restrict_vector<16>(weights); for (int y=0; y < 6; y++) { for (int x=0; x < 6; x++) { acc = aie::mac(acc, aie::broadcast<bfloat16,16>((*(it+y)).get(x+cc)), *itw++); } // x } // y acc = aie::add(acc, aie::load_v<16>(biases)); convs[i] = aie::max(acc.to_vector<bfloat16>(),bfloat16(0)); conv_num++; } // cc it += 2; // or rr } // rr *out = aie::max(aie::max(convs[0],convs[1]), aie::max(convs[2],convs[3]));}Now this is still not quite right.
The careful reader may have noticed a type mismatch between uint8 and bfloat16. In the real system I’m working on,
the input is indeed uint8, but it’s exclusively ones and zeroes, so we can optimize a bit by dropping the MAC calls entirely and simply adding the
weights to the accumulator conditionally on whether we have a one or a zero. Technically the vector iterator of size 8 for uint8 also doesn’t exist,
so in the real code I used a 16 iterator and the y loop only happens 3 times, but those are just implementation details.
Another benefit of this kernel is that it’s agnostic with respect to the section from the input, so it’s easy to add copies of it working in parallel, in fact, that’s exactly what I did with the final graph:
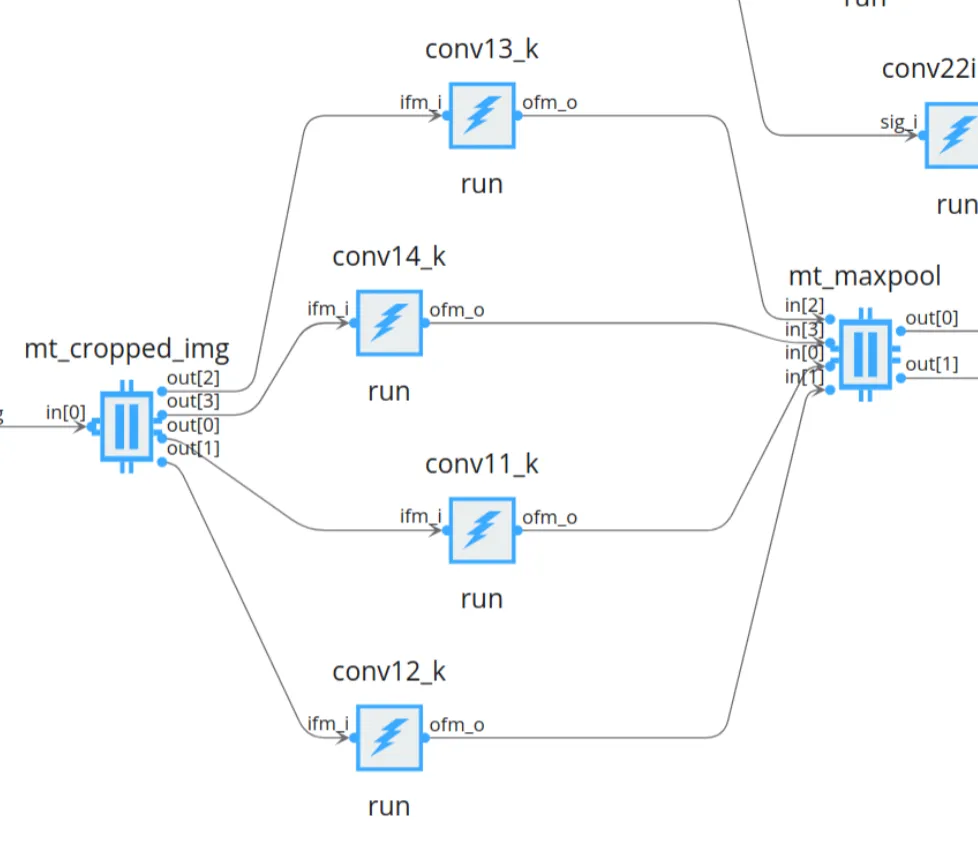
I hope to talk about this full design in more detail next time, as we managed to benchmark (about 3x) faster inference than the NVIDIA Jetson with this chip!